GPT-5.2 ProがErdős問題を解決:AIが数学研究を変える転換点
2026年1月、人工知能による科学的発見の能力が新たなフェーズに突入しました。OpenAIの最新モデル「GPT-5.2 Pro」が、30年以上にわたり未解決だった数学問題「Erdős(エルデシュ)問題#397」を解決し、フィールズ賞受賞者テレンス・タオ氏による検証を受けたのです。

この成果は、AIが単なる情報検索ツールではなく、厳密な論理構築と新規性が求められる純粋数学の証明において、人間に匹敵する推論能力を持つことを実証しました。そして、この技術は数学の世界にとどまらず、企業における複雑な論理的問題解決への応用が期待されています。
30年来の未解決問題が解決された瞬間
ポール・エルデシュ(Paul Erdős, 1913-1996)は、20世紀を代表する数学者であり、生涯に数多くの未解決問題を提起しました。彼は問題の難易度に応じて賞金を設定しており、これらは数学者にとっての「挑戦状」として機能してきました。
Erdős問題#397は、中心二項係数(central binomial coefficients)に関わるディオファントス方程式の解の存在性に関する問題です。中心二項係数は で表され、パスカルの三角形の中央に位置する数で、数論において重要な性質を持ちます。
2026年1月9日から11日にかけて、Neel Somani氏らの試みにより、GPT-5.2 Proがこの問題を含む複数のErdős問題を解決しました。特筆すべきは、自然言語による証明の生成だけでなく、コンピュータが検証可能な形式言語(Lean)による実装までがAI主導で行われた点です。
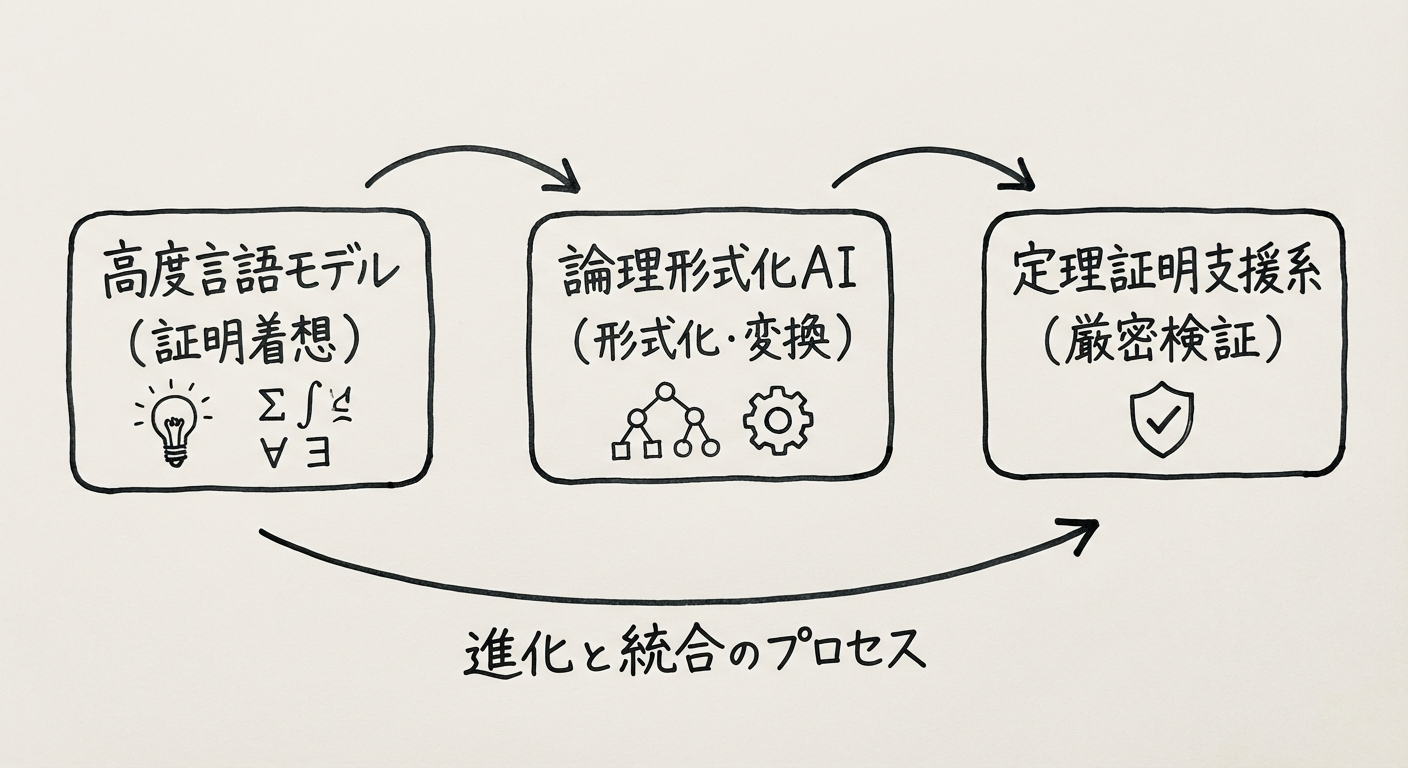
図1: GPT-5.2 ProとAristotleによる数学的証明プロセス
3つのAIがタッグを組んだ証明プロセス
今回の解決は、単一のAIモデルによる出力ではなく、高度な推論モデルと形式検証ツールの連携によって達成されました。
使用された技術スタック
GPT-5.2 Pro(OpenAI) は、証明のアイデアと構成を担当しました。推論能力(Reasoning Effort)が「xhigh(極めて高い)」に設定されており、複雑な多段階推論や科学的評価に最適化されています。最大40万トークンのコンテキストウィンドウを持ち、長大な数学的議論を維持可能です。
Aristotle(Harmonic) は、形式化と検証を担当しました。GPTが生成した自然言語の証明を、定理証明支援系言語「Lean」のコードに変換し、論理的ギャップを埋める役割を果たしました。数学に特化したAIエージェントであり、証明の欠落部分を自動修正し、Leanコンパイラが通るまで試行錯誤を行う能力を持ちます。
Lean(Proof Assistant) は、最終的な検証を担当しました。人間が査読するのではなく、コンピュータプログラムとして論理の正しさを絶対的に保証します。
解決のステップ
証明プロセスは以下の5つのステップで進行しました。
- プロンプト入力: ユーザーがGPT-5.2 Proに対し、Erdős問題#397の定義を与え、解決を指示
- 証明の生成: GPT-5.2 Proが中心二項係数に関する恒等式を発見し、それが問題の解法に繋がることを特定。自然言語とLaTeX形式で証明の概略を出力
- 形式化と修正: 生成された証明をAristotleに入力。Leanコードに変換しようと試みる過程で、論理の飛躍や軽微なエラーを検出し、自律的に修正
- 検証完了: Leanによるコンパイルが成功し、数学的に矛盾がないことが証明
- 提出: 結果がテレンス・タオ氏に送られ、確認
このプロセスにおいて、GPT-5.2 Proは「証明のアイデア(What)」を出し、Aristotleが「厳密な検証(How)」を担当するという分業が成立しています。
フィールズ賞受賞者による検証が意味するもの
フィールズ賞受賞者であり、現代最高の数学者の一人とされるテレンス・タオ(UCLA教授)の関与は、本件の信頼性を担保する決定的な要素です。
タオ氏は、GitHub上で「AI contributions to Erdős problems」というプロジェクトを運営しており、AIによる成果を追跡・検証しています。彼は、GPT-5.2 ProとAristotleによって生成された#397の証明を受け入れ、その有効性を認めました。
タオ氏の評価ポイントは2つあります。まず、オリジナリティです。既存の文献を単にコピーしたものではなく、AIが問題の意図を汲み取り(再構成し)、論理を構築した点を評価しています。次に、形式的検証の価値です。Leanによる検証が通っていることは、人間の査読以上の厳密さを提供します。タオ氏は、AIが証明の細部を埋め、人間がより高次の概念に集中できる可能性を示唆しています。
タオ氏はAIに対して過度な期待を戒める立場をとっており、「AIは数学者ではない」「神格化をやめるべき」と警鐘を鳴らしています。そのような慎重な立場をとる第一人者が、今回の成果を「マイルストーン」として認めたことは、この解決が単なる偶然やトリックではないことを裏付けています。
「Erdősgate」騒動との決定的な違い
今回の成果を正しく評価するためには、数ヶ月前に発生した「Erdősgate(エルデシュゲート)」と呼ばれる騒動との違いを理解する必要があります。
2025年10月、OpenAIのGPT-5(当時)が「未解決のErdős問題を解いた」と主張されましたが、後に以下の事実が判明し、批判を浴びました。
AIが「解いた」とした問題は、実際には既に人間によって解決済みであり、単に特定のデータベースに「解決済み」として反映されていなかっただけでした。AIは新しい証明を作ったのではなく、既存の文献を見つけてきた(あるいは文献の内容を再出力した)に過ぎませんでした。さらに、一部のケースでは、存在しない証明をでっち上げていました。
今回のGPT-5.2 Proによる#397の解決は、以下の点で前回とは異なります。
自律的な論理構築: タオ氏やコミュニティの調査により、今回の証明と同じロジックを用いた文献は発見されていません(類似の手法は存在するが、直接的な解決は新規)。
Leanによる完全検証: 自然言語の曖昧さを排除するLeanコードが生成され、コンパイルが通っています。これは「幻覚」ではないことの数学的証明です。
問題の再構成: 問題文に曖昧さがあった場合、AIがその「意図(spirit)」を解釈し、数学的に意味のある形に再定義して解いた事例も含まれており、単なる検索以上の知能を示しています。
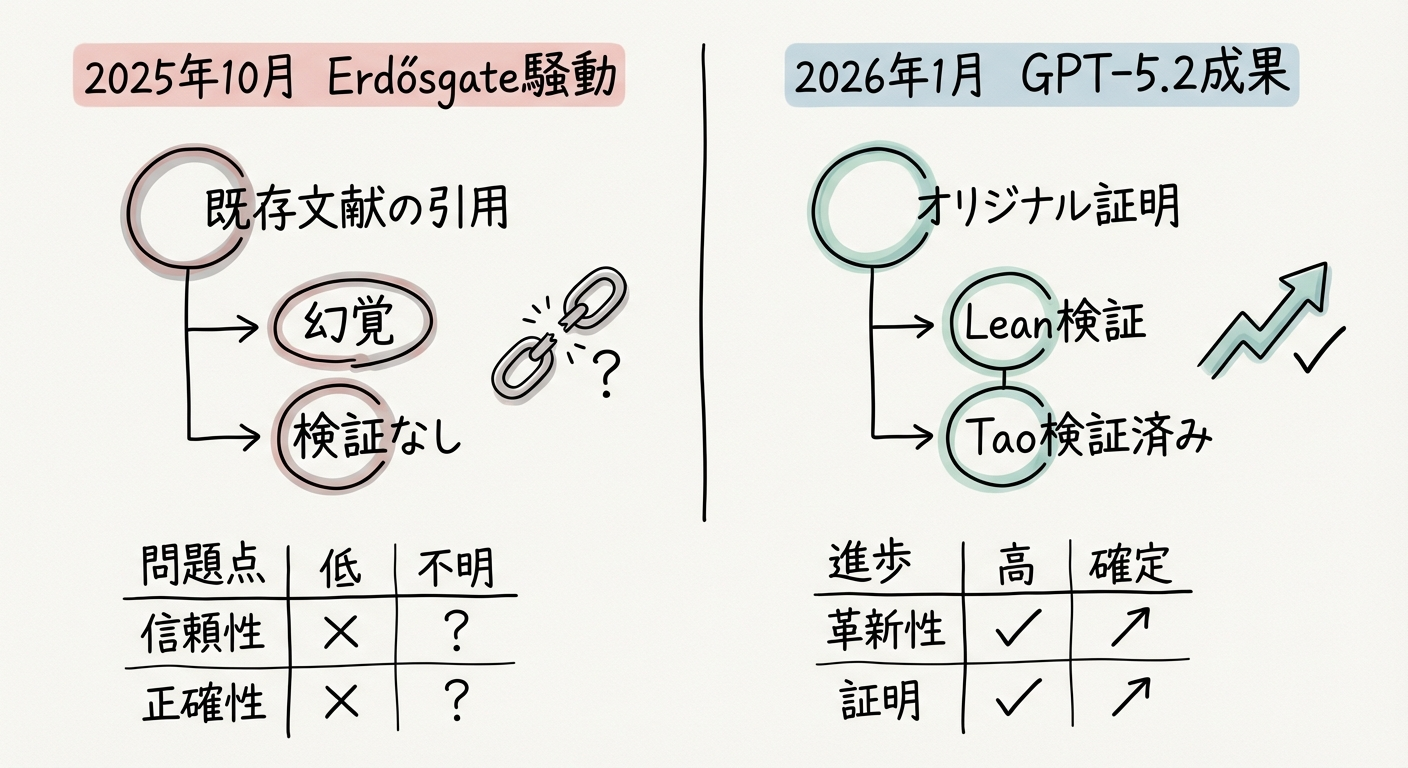
図2: 2025年10月の騒動と今回の成果の決定的な違い
PSVループ:AIが科学的発見を自律化する
本件は「Propose(提案), Solve(解決), Verify(検証)」というPSVループがAI単独(または人間との最小限の協力)で回ることを実証しました。
Propose(提案) では、人間が問題を与える(あるいはAIが関連問題を探索する)ことから始まります。Solve(解決) では、GPT-5.2 Proが証明の概略を作ります。そしてVerify(検証) では、Aristotle/Leanが厳密性を保証します。
このサイクルにより、人間が見落としていた「標準的な難問」や、計算量が膨大で人間が敬遠していた問題が次々と解決される可能性があります。
graph LR
A[Propose<br/>問題の提案] --> B[Solve<br/>GPT-5.2 Proによる解決]
B --> C[Verify<br/>Aristotle/Leanによる検証]
C --> D{検証成功?}
D -->|No| B
D -->|Yes| E[証明完了]
企業における数学的証明の応用可能性
数学的証明の能力は、学術の世界にとどまらず、ビジネスにおける論理的検証に応用可能です。
形式検証の産業応用
金融工学では、デリバティブの価格付けモデルの検証にGPT-5.2 ProとLeanのような形式検証ツールの組み合わせが導入されるでしょう。金融商品の複雑な数理モデルが数学的に正しいことを自動的に検証できれば、リスク管理の精度が飛躍的に向上します。
サイバーセキュリティでは、暗号プロトコルの安全性証明に活用できます。暗号アルゴリズムが理論的に破られないことを数学的に証明することで、より安全な通信インフラが実現します。
ソフトウェア開発では、バグのないコードの保証に使えます。プログラムの論理的正しさを形式的に検証することで、クリティカルなシステムの信頼性を担保できます。航空機の制御システムや医療機器のソフトウェアなど、人命に関わるシステムでは特に重要です。
複雑な最適化問題の解決
物流、製造ライン、電力網などの最適化問題において、AIが数理モデルを構築し、その解の正当性を数学的に保証するプロセスが自動化される可能性があります。
日本の製造業やインフラ企業にとって、これは生産性向上の大きな鍵となります。例えば、工場の生産スケジューリングや配送ルートの最適化において、AIが生成した解が最適であることを数学的に証明できれば、経営判断の確実性が大幅に向上します。
日本の研究・産業への示唆
日本は伝統的に数論や代数幾何学などの分野で世界的な実績を持っています。日本の数学者がGPT-5.2 ProやLeanのようなツールを導入することで、証明の検証にかかる時間を大幅に短縮できる可能性があります。特に、若手研究者が自身の直感を素早く検証するためのパートナーとしてAIを活用することが期待されます。
日本の科学技術政策における「選択と集中」が批判される中、AIは「注目されていないが重要な問題(ロングテール)」を低コストで解決する手段となり得ます。これにより、資金が集中しない分野でも成果が出せるようになり、研究の多様性が保たれる可能性があります。
AIと数学者の共進化
専門家は、今回解かれた問題が標準的な手法の組み合わせで解けるものであり、新しい数学的概念や深い洞察(Deep Insight)を必要とするものではないと指摘しています。テレンス・タオ氏は、これらを「低い位置にある果実(lowest hanging fruit)」と表現しています。
完全に自律的とは言えず、人間による適切なプロンプトや、形式化ツールへの入力といった「導き」が必要です。また、AIは「なぜその問題が重要か」という文脈や美学を理解しているわけではありません。
しかし、これは限界というよりも、人間とAIの役割分担を示唆しています。数学者の役割は、「証明を書くこと」から「証明すべき重要な問題を定義すること」や「AIが生成した証明の意味を解釈し、より大きな理論体系に位置づけること」へとシフトしていくでしょう。
Erdős問題はまだ600以上残されています。今後数ヶ月(6〜12ヶ月)の間に、GPT-5.3やGoogle/Anthropicの競合モデルが、これらの中の「計算量で解決できる問題」や「標準的手法の組み合わせで解ける問題」を体系的に攻略していくと予想されます。
まとめ
GPT-5.2 ProによるErdős問題#397の解決は、AIが「計算機」から「推論機」へと進化したことを示す歴史的な転換点です。それは人間から数学の仕事を奪うものではなく、数学的探求のフロンティアを拡張する強力なパートナーの誕生を意味します。
テレンス・タオ氏による検証は、この技術が学術的に耐えうる水準に達しつつあることを保証しました。そして、この技術は学術の世界にとどまらず、企業における金融工学、サイバーセキュリティ、ソフトウェア開発、最適化問題など、さまざまな分野での論理的検証に応用可能です。
日本においても、この技術をいち早く研究や産業に取り入れることが、次世代の競争力を左右することになるでしょう。AIと人間の共進化による、新たな知的創造の時代が始まっています。
AI COMMONでは、最新のAI技術を活用した論理的問題解決やシステム構築から運用まで、トータルでサポートしています。 数学的証明技術の産業応用や、AIによる複雑な問題解決についてご検討の方は、お気軽にお問い合わせください。
関連記事
参考文献
-
The Neuron Daily "AI Cracks Legendary Erdős Problems"
https://www.theneurondaily.com/p/ai-cracks-legendary-erdos-problems -
OpenAI "GPT-5.2 for Science and Math"
https://openai.com/index/gpt-5-2-for-science-and-math/ -
Terence Tao (Mathstodon) "AI contributions to Erdős problems"
https://mathstodon.xyz/@tao/ -
ByteIota "GPT-5.2 Solves Erdős Math Problem: But Did It Really?"
https://byteiota.com/gpt-5-2-solves-erdos-math-problem-but-did-it-really/ -
OpenAI "Mathematical Discovery with GPT-5"
https://openai.com/index/gpt-5-mathematical-discovery/